BONSAJOVÁ ŠKOLA I. - Zlatý rez

BONSAJOVÁ ŠKOLA I. Zlatý rez
článok z magazínu
Bonsaj a čaj č. 1/2004

Text a foto:
RNDr. Vladimír Ondejčík, RNDr. Alena Ondejčíková
Bonsai Slovakia, Nitra,

BEZ MATEMATIKY NIET UMENIA
– povedal Luca Pacioli a my začíname našu bonsajovú školu malou hodinou matematiky. Žeby sa krása dala vypočítať?
Je to podivné, ale zdá sa, že áno. Vo veciach, ktoré sa nám javia ako neodolateľne krásne, ba dokonca i v prirodzenej stavbe tiel rastlín, živočíchov i človeka, sa opakujú viace-ré matematické zákonitosti. A ich vzájomná geometrická harmónia v duši človeka vyvoláva pocit krásna.

DIVINA PROPORTIO
Najtajomnejšou matematickou zákonitosťou je „Divina proportio = božský pomer“ alebo známy „zlatý rez“. To sú rôzne názvy toho istého pomeru alebo čísla, vďaka ktorému nás niektoré umelecké diela uchvacujú a iné nie. Cítime, že im niečo ťažko definovateľné chýba. Kľúčom k pochopeniu býva práve zlatý rez.

EUKLIDES
Už 340 rokov pred naším letopočtom antický matematik Euklides po-znal význam zlatého rezu, ba priam mu pripisoval „božskú“ moc. Vo svojej knihe Základy, z ktorej sa učilo a učí dodnes (!), opísal konštrukciu zlatého rezu.

Bola riešením tejto úlohy:
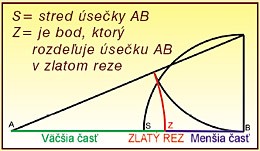
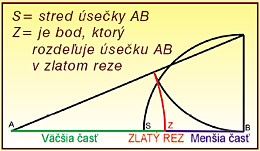
„Rozdeľ úsečku na dve časti tak, aby obdĺžnik, ktorého jedna strana je celá úsečka a druhá jeden z jej dielov, mal rovnaký obsah ako štvorec nad druhým dielom”. Čo významovo je to isté ako úloha:
„Rozdeľte úsečku na dve časti tak, aby pomer dĺžok malej časti k veľkej časti bol taký istý, ako veľkej časti
k celku. Výsledkom tejto úlohy je iracionálne číslo 1,618033988... 

FIBONACCI
Predbehol dobu o niekoľko storočí. Žil v rokoch 1170 -1250 a bol matematikom, cestovateľom po Oriente i obchodníkom. Do Európy priniesol arabskú matematiku i arabské číslice. Desiatková sústava, ktorú používame každý deň, sa zachovala práve vďaka jeho knihe Algorizmi de numero indozum - O indickom čísle od Algorizmiho. Je zaujímavé, že arabský originál odvial čas a pre nás sa zachoval len latinský preklad od Fibonacciho.

POČÍTANIE KRÁLIKOV
Prečo práve Fibonaccimu venujeme toľko pozornosti? Pretože, keď tento geniálny matematik riešil prozaickú "sedliacku" úlohu "koľko párov králikov sa počas jedného roku narodí z jedného páru, ak každý pár dá za mesiac prírastok jeden pár, pričom bude schopný plodiť po dvoch mesiacoch a žiadny pár nezahynie?", prišiel na zaujímavú postupnosť čísel: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, ..., v ktorej každé nasledujúce číslo sa rovná súčtu dvoch predchádzajúcich. Pre nás je "Fibonacciho postupnosť" zaujímavá najmä tým, že pomer susedných čísiel vystihuje princíp zlatého rezu a to tým presnejšie, čím sú čísla väčšie. 1:2, 2:3, 3:5, 5:8, 8:13...
Fibonacci pochádzal zo známeho talianskeho mesta Pisa a vlastným menom sa volal Leonardo Pisanský. Odkiaľ prišlo meno Fibonacci? Leonardo bol synom pisára, diplomatického úradníka Guilielma Bonaccia a meno FIBONACCI znamená v taliančine "syn Bonaccia". Narodil sa v Taliansku, ale učil sa v severnej Afrike, kde jeho otec zastupoval záuj-my Republiky Pisa. Toto talianske mesto malo výbornú polohu a veľmi aktívne obchodné kontakty so sever-nou Afrikou i Blízkym východom.
Knihy Liber Quadratorum (Kniha štvorcov), ktorá je venovaná algebre, Praktica geometriae (Prax geometrie), v ktorej píše o Euklidovskej geomet-rii, i kniha o aritmetike Liber abaci (Kniha o abaku) boli veľkým prínosom pre ďalšie matematické objavy. A práve v tretej časti knihy Liber abaci sa stretávame so slávnou "Fibonacciho postupnosťou" čísiel, ktorá nás vedie k zlatému rezu, tak dôležitému pre tvorbu krásnych bonsajov.

ZLATÝ REZ
Ako si prakticky predstaviť zlatý rez? Ak rozdelíme obraz, fotografiu alebo iné umelecké dielo pomyselne v pomere čísel vychádzajúcich z Fibonacciho postupnosti, napr. 1:2 alebo 2:3, ťažisko alebo hlavný motív by mal byť umiestnený čo najbližšie k tejto línii.
Ak napríklad strom zasadíme symetricky presne do stredu misky, bude pôsobiť neprirodzene staticky a nudne, ak toto umiestnenie nepodlieha inému zámeru. Pri umiestnení mierne asymetricky približne 1/3 od okraja, akoby náhle ožil. Rovnako napríklad pri fotografovaní hlavný motív neumiestňujeme presne do stredu fotky, ale mierne bokom - čo najbližšie k zlatému rezu a cesta do duše sa náhle otvára...

LEONARDO DA VINCI
Bol znalcom geometrie, študoval podrobne i mate-matické zákonitosti ľudského tela a aj v maľbách využíval okrem svojho mi-moriadneho výtvarného talentu aj svoje vynikajúce matematické schopnosti. Zlatý rez nielen poznal, ale aj uplatňoval. Obdobie renesancie vôbec bolo obdobím "zlatého rezu" v umení. Zachovalo sa mnoho maliarskych štúdií ľudského tela podľa zlatého rezu. I hlavný motív sa umiestňoval často presne do zlatého rezu obrazu.

MONA LISA
Stáli sme pred ňou v parížskom Louvri a dívali sme sa jej do očí. Usmievala sa v bleskoch fotoaparátov japonských turistov a ničím, vôbec ničím sa do pozornosti divákov nevtierala. Žiadne šperky, ozdoby, pestré farby... A predsa sa vliala priamo do našich duší ako jeden z fascinu-júcich divov sveta. Prielom vesmírov. Absencia plynutia času. Samadhi. Slová stratili význam a dôležitosť...
Rozmery obrazu Mony Lisy zodpovedajú presne zlatému rezu. A hoci je hlavný motív zdanlivo v strede obrazu, zlatý rez sa opakuje v stovkách jednotlivých detailov tohoto nezabudnuteľného diela, ktoré si nadovšetko vážil i jeho autor Leonardo da Vinci a kamkoľvek cestoval, Mona Lisa bola vždy po jeho boku.

BONSAJE A ZLATÝ REZ
Tak ako starí egyptskí i grécki stavitelia, sochári, či renesanční maliari využívali zlatý rez, tak je aj v tvorbe bonsajov hlavným oporným bodom. Ak chceme vytvoriť majstrovské dielo, ktoré v ľuďoch vyvolá hlboké vnemy a zážitky, je správne nielen sa nechať viesť intuíciou, ale tvarovať stromy s hlbokým poznaním matematických pomerov a zákonitostí. A to nielen pri sadení stromu do misky, ale aj pri rozložení a stavbe koruny, umiestnení jednotlivých vetiev, ich výšky a šírky stromu, tvaru kmeňa... Nechceme vás hneď na začiatku od tvorby bonsajov odradiť, ale vás citlivo, krôčik po krôčiku voviesť do nádhernej rozprávkovej ríše poznania a citu.

JOHN YOSHIO NAKA
Patrí k najvýznamnejším popularizátorom klasickej japonskej bonsajovej školy 20. storočia a svojou tvorbou i výukou ovplyvnil mnohých ďalších výnimočných bonsajistov svetového formátu. Jeho bonsaje i krajinné scenérie sú mimoriadne vyvážené a pôsobivé, pretože v nich temer striktne dodržiaval pravidlá, vďaka ktorým je japonská estetika taká pôsobivá.
Ako jeden z prvých učil bonsajistiku na základe geometrických konštrukcií a aritmetických vzorcov. Princíp zlatého rezu sa objavoval v každom detaile jeho bonsajov - skutočných umeleckých diel. John Naka vďaka tomuto svojmu matematickému prístupu urobil umenie tvorby bonsajov zrozumiteľným pre všetkých ľudí bez rozdielu národnosti, mentality, či farby pleti a dal tak bonsajistike punc celosvetového umeleckého smeru. Vďaka pochopeniu univerzálnych princípov prestali byť bonsaje čudnými prvkami cudzej kultúry, ale stali sa kultúrnym dedičstvom celej planéty.

MASAHIKO KIMURA
Je súčasným umelcom najvyššieho formátu. Jeho bonsaje majú zvláštny rukopis, sú jednoducho neopakovateľné. Práve pre tento svojský a odvážny prístup si vyslúžil titul "Bonsajový génius". Hoci vo svojej tvorbe láme tradície a jeho expresívne umenie hlboko burcuje i uchvacuje ľudského ducha, v jeho stromoch sa dá na prvý pohľad odhaliť mnoho matematických zákonitostí, najmä princíp zlatého rezu, ktorý sa opakuje v mnohých častiach každého jeho diela. Pozrime sa napríklad na nety-pickú krajinnú scenériu vysadenú na šikmých keramických "škrupinách".
Koľko symetrie a pravidelnosti je v tomto asymetrickom diele, ktoré sme pre vás odfotografovali priamo v záhrade majstra Kimuru! Napríklad dominantný strom sa nachádza presne v zlatom reze celej kompozície, malá keramická škrupinka je predelená v zlatom reze, horné okraje oboch škrupín sú v zlatom reze i križujú sa v zlatom reze a to isté platí o jednotlivých stromoch i o ich menších celkoch. Podobne ako v obraze Mony Lisy.

TAJOMNÝ PRIELOM KU KRÁSE
Vidíme, že zlatý rez - samozrejmá súčasť Euklidovskej geometrie, má svoje uplatnenie vo výtvarnom, fotografickom, ale aj bonsajovom umení. Zlatý rez nie je fixná doména. Je to tajomný prielom k bodu, ktorý naša duša pociťuje ako krásno. Je to i jednoduchá pomôcka, ktorá nám uľahčuje základnú orientáciu. Nechajme sa teda inšpirovať vlastnou fantáziou, možnosťami dreviny, ktorú chceme premeniť na bonsaj, a zároveň nezabúdajme toto prvé univerzálne pravidlo nášho bytia. 

© Magazín BONSAJ A ČAJ

Viac obrázkov a zaujímavostí nájdete na stránkach kvalitného plnofarebného magazínu Bonsaj a čaj.